🚧 This website is under construction. 🚧
AtCoder
蟻本
2-3

2-3 値を覚えて再利用 "動的計画法"

探索のメモ化と動的計画法

# 01ナップサック問題 (ナイーブ解)
n: int = 4
w: list[int] = [2, 1, 3, 2]
v: list[int] = [3, 2, 4, 2]
W: int = 5
 
 
def rec(i, j) -> int:
    """
    iは選択済みの商品番号、jはナップサックの残用量
    """
    if i == n:
        return 0
    return max((v[i] + rec(i + 1, j - w[i])) * (j >= w[i]), rec(i + 1, j))
 
 
def solve() -> None:
    print(rec(0, W))

ナイーブ解の計算量

探索の深さは最大nn、各深さにおいて 2 回分岐するため、計算量は O(2N)O(2^N)

∑i=0n2i=2(1−2n)1−2=2(2n−1)=O(2n)\sum_{i=0}^{n}2^{i}=\frac{2(1-2^{n})}{1-2}=2(2^{n}-1)=O(2^n)

ナイーブ解の改善

rec(i, j) の呼び出しにおける (i, j) の組み合わせは高々 nWnW 通りなので、呼び出し結果を保存しておくことで計算量を改善できる。

## 01ナップサック問題 (メモ化)
 
import functools
 
 
@functools.cache
def rec(i: int, j: int) -> int:
    if i == n:
        return 0
    return max(v[i] + rec(i + 1, j - w[i]) * (j >= w[i]), rec(i + 1, j))
 
 
def solve() -> None:
    print(rec(0, W))
 
## 01ナップサック問題 (メモ化ー自力で実装)
 
memo: list[list[int]] = [[-1] * (W + 1) for _ in range(n)]
 
 
def rec(i: int, j: int) -> int:
    if not memo[i][j] != -1:
        return memo[i][j]
    if i == n:
        return 0
    memo[i][j] = max((v[i] + rec(i + 1, j - w[i])) * (j >= w[i]), rec(i + 1, j))
    return memo[i][j]
 
 
def solve() -> None:
    print(rec(0, W))

メモ化後の計算量

引数の組み合わせは高々 nWnW 通りであり、関数内でも 2 回の再帰呼び出しが行われるのみであるから、計算量は O(nW)O(nW)。

そして DP へ

dp[i][j] は関数 rec(i, j) の定義より、i 番目の品物以降の品物から重さの総和が j 以下となるように選んだときの価値の総和となっている。値は次のように計算できる。

dp[n][j]=0dp[i][j]={dp[i+1][j](j<w[i])max⁡(dp[i+1][j],dp[i+1][j−w[i]]+v[i])(otherwise)\begin{aligned} dp[n][j] &= 0\\ dp[i][j] &= \begin{cases} dp[i + 1][j] & (j < w[i])\\ \max(dp[i+1][j], dp[i+1][j-w[i]]+v[i]) & (\text{otherwise}) \end{cases} \end{aligned}

この計算式を用いることで、単純な 2 重ループで問題を解く事が出来る。

# 01ナップサック問題（DP・逆方向）
 
n = 4
w = [2, 1, 3, 2]
v = [3, 2, 4, 2]
W = 5
 
dp = [[-100 for _ in range(W + 1)] for _ in range(n + 1)]
for j in range(W + 1):
    dp[n][j] = 0
 
for i in reversed(range(n)):
    for j in range(W + 1):
        if j < w[i]:
            dp[i][j] = dp[i + 1][j]
        else:
            dp[i][j] = max(dp[i + 1][j], dp[i + 1][j - w[i]] + v[i])
i ＼ j012345
0-100-100-100-100-100-100
1-100-100-100-100-100-100
2-100-100-100-100-100-100
3-100-100-100-100-100-100
4-100-100-100-100-100-100

漸化式は次のように定める事も出来る。

dp[0][j]=0dp[i+1][j]={dp[i][j](j<w[i])max⁡(dp[i][j],dp[i][j−w[i]]+v[i])(otherwise)\begin{aligned} dp[0][j] &= 0\\ dp[i+1][j] &= \begin{cases} dp[i][j] & (j < w[i])\\ \max(dp[i][j], dp[i][j-w[i]]+v[i]) & (\text{otherwise}) \end{cases} \end{aligned} 
## 01ナップサック問題（DP・順方向）
 
n = 4
w = [2, 1, 3, 2]
v = [3, 2, 4, 2]
W = 5
 
dp = [[-100 for _ in range(W + 1)] for _ in range(n + 1)]
for j in range(W + 1):
    dp[0][j] = 0
 
for i in range(n):
    for j in range(W + 1):
        if j < w[i]:
            dp[i + 1][j] = dp[i][j]
        else:
            dp[i + 1][j] = max(dp[i][j], dp[i][j - w[i]] + v[i])
i ＼ j012345
0-100-100-100-100-100-100
1-100-100-100-100-100-100
2-100-100-100-100-100-100
3-100-100-100-100-100-100
4-100-100-100-100-100-100

実際の DP はどう考えるのか

  1. DP テーブルの定義
  2. 遷移式
  3. 埋める方向

最長共通部分列問題(LCS)

dp[i][j]:=The length of LCS for s1...si and t1...tjdp[0][0]=0dp[i+1][j+1]={max⁡(dp[i][j]+1,dp[i][j+1],dp[i+1][j])(Si+1=tj+1)max⁡(dp[i][j+1],dp[i+1][j])(otherwise)\begin{aligned} dp[i][j] &:= \text{The length of LCS for } s_1...s_i \text{ and } t_1...t_j \\ dp[0][0] &= 0\\ dp[i+1][j+1] &= \begin{cases} \max(dp[i][j]+1, dp[i][j+1], dp[i+1][j]) & (S_{i+1}=t_{j+1}) \\ \max(dp[i][j+1], dp[i+1][j]) & (\text{otherwise}) \end{cases} \end{aligned}

ポイントは、遷移における矢印の意味が文字を足すではなく、文字を消す操作に対応するということである。

文字列の入ったスタックから、任意の順番で文字を取り出していく操作だと見なすと分かりやすい。

LCS1

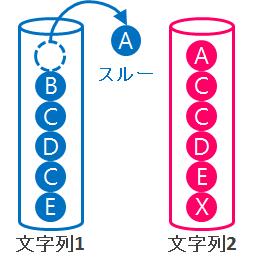
どちらか一方のスタックから要素を取り出す操作では文字のマッチは考えない。これは DP テーブルでの右方向または下方向への遷移に対応する。

LCS2

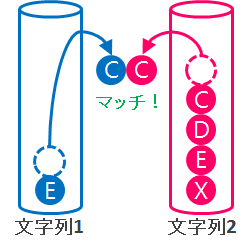
両方の要素を同時に取り出すときに、そのタイミングで文字をマッチさせる(LCSを構成する要素)と考える。これは DP テーブルでの右下方向への遷移に対応する。

【画像引用】まくろぐ / 文字列の類似度を計算する (LCS: 最長共通部分列) (opens in a new tab)

# 最長共通部分問題
 
n: int = 4
m: int = 4
s: str = "abcd"
t: str = "becd"
 
# dp[i][j] := s[:i], t[:j] での LCS の長さ
dp: list[list[int]] = [[0 for _ in range(m + 1)] for _ in range(n + 1)]
 
film = [copy.deepcopy(dp)]
for i in range(n):
    for j in range(m):
        dp[i + 1][j + 1] = max(dp[i + 1][j], dp[i][j + 1], dp[i][j] + (s[i] == t[j]))
        film.append(copy.deepcopy(dp))
 
 
@ipywidgets.interact(flame=ipywidgets.IntSlider(min=0, max=len(film) - 1))
def show_table_transition(flame: int):
    table = pd.DataFrame(
        film[flame], columns=list(enumerate(" " + s)), index=list(enumerate(" " + t))
    )
    with pd.option_context("display.float_format", "{:.0g}".format):
        display(table)

漸化式を工夫する

個数制限なしナップサック問題

dp[i][j]:=i番目までの品物から、重さの総和がj以下になるように選んだときの価値の総和の最大値dp[0][j]=0dp[i+1][j+1]=max⁡(dp[i][j−k×w[i]]+k×v[i]∣0≦k)\begin{aligned} dp[i][j] &:= i番目までの品物から、重さの総和がj以下になるように選んだときの価値の総和の最大値 \\ dp[0][j] &= 0\\ dp[i+1][j+1] &= \max ({dp[i][j-k \times w[i]]+k\times v[i] | 0\leqq k}) \end{aligned} 
# 個数制限なしナップサック問題 (ナイーブ解)
n: int = 3
w: list[int] = [3, 4, 2]
v: list[int] = [4, 5, 3]
W: int = 7
 
dp: list[list[int]] = [[0 for _ in range(W + 1)] for _ in range(n + 1)]
 
film = [(copy.deepcopy(dp), (0, 0, 0))]
for i in range(n):
    for j in range(W + 1):
        for k in range(j // w[i] + 1):
            dp[i + 1][j] = max(dp[i + 1][j], dp[i][j - k * w[i]] + k * v[i])
            film.append((copy.deepcopy(dp), (i, j, k)))
 
 
@ipywidgets.interact(flame=ipywidgets.IntSlider(min=0, max=len(film) - 1))
def show_table_transition(flame: int):
    dp, (i, j, k) = film[flame]
    table = pd.DataFrame(dp)
    with pd.option_context("display.float_format", "{:.0g}".format):
        display(
            table.style.set_properties(
                subset=pd.IndexSlice[i + 1, j], **{"background-color": "#FF7000"}
            ).set_properties(
                subset=pd.IndexSlice[i, j - k * w[i]], **{"background-color": "#FFBF00"}
            )
        )
        print(f"価値{v[i]}、重さ{w[i]}の品物を{k}個取る")

ナイーブ解の計算量改善

dp[i+1][j]dp[i+1][j] の計算において、k(≧1)k(\geqq1) 個選ぶ場合は dp[i+1][j−w[i]]dp[i+1][j-w[i]] の計算において k−1k-1 個選んだ場合と同様であるため、 dp[i+1][j]dp[i+1][j] の遷移式における k≧1k\geqq1 の部分の計算は既に dp[i+1][j−w[i]]dp[i+1][j-w[i]] の計算時に行っている。

つまり、次のような式変形が可能

# 個数制限なしナップサック問題 (計算量改善)
n: int = 3
w: list[int] = [3, 4, 2]
v: list[int] = [4, 5, 3]
W: int = 7
 
dp: list[list[int]] = [[0 for _ in range(W + 1)] for _ in range(n + 1)]
 
film = [(copy.deepcopy(dp), (0, 0, 0))]
for i in range(n):
    for j in range(W + 1):
        dp[i + 1][j] = max(dp[i][j], dp[i + 1][j - w[i]] + v[i] * (j - w[i] >= 0))
        film.append((copy.deepcopy(dp), (i, j, k)))
 
 
@ipywidgets.interact(flame=ipywidgets.IntSlider(min=0, max=len(film) - 1))
def show_table_transition(flame: int) -> None:
    dp, (i, j, k) = film[flame]
    table = pd.DataFrame(dp)
    with pd.option_context("display.float_format", "{:.0g}".format):
        table = table.style.set_properties(
            subset=pd.IndexSlice[i + 1, j], **{"background-color": "#FF7000"}
        ).set_properties(subset=pd.IndexSlice[i, j], **{"background-color": "#FFBF00"})
        if j - w[i] >= 0:
            table = table.set_properties(
                subset=pd.IndexSlice[i + 1, j - w[i]], **{"background-color": "#FFBF00"}
            )
        display(table)
        if j - w[i] >= 0:
            print(f"{v[i]:+}")

配列の再利用

...

01 ナップサック問題その 2

価値の総和を最大化すること <=> 重さの総和を最小化すること

dp[i][j]:=i番目までの品物から、価値の総和がjとなるように選んだときの重さの総和の最小値dp[0][j]=∞(j>0)dp[0][0]=0dp[i+1][j+1]=min⁡(dp[i][j],dp[i−v[i]]+w[i])\begin{aligned} dp[i][j] &:= i番目までの品物から、価値の総和がjとなるように選んだときの重さの総和の最小値 \\ dp[0][j] &= \infty (j > 0)\\ dp[0][0] &= 0 \\ dp[i+1][j+1] &= \min(dp[i][j], dp[i-v[i]]+w[i]) \\ \end{aligned} 
# コードは省略

個数制限付き部分和問題

dp[i][j]:=i番目まででjが作れるかdp[i][j]=any({dp[i][j−k×ai]∣0≤k≤miかつk×ai≤j})\begin{aligned} dp[i][j] &:= i番目まででjが作れるか \\ dp[i][j] &= any(\{dp[i][j-k\times a_{i}] | 0\le k\le m_{i}かつk\times a_{i}\le j\}) \end{aligned}

計算時間は O(K∑imi)\mathcal{O}(K\sum_{i}m_{i})

# 個数制限付き部分和問題（ナイーブ解）
 
n: int = 3
K: int = 17
a: list[int] = [3, 5, 8]
m: list[int] = [3, 2, 2]
 
dp: list[list[int]] = [[False for _ in range(K + 1)] for _ in range(n + 1)]
dp[0][0] = True
 
film = [(copy.deepcopy(dp), (0, 0, 0))]
for i in range(n):
    for j in range(K + 1):
        for k in range(K + 1):
            if not (0 <= k <= m[i] and k * a[i] <= j):
                break
            dp[i + 1][j] |= dp[i][j - k * a[i]]
            film.append((copy.deepcopy(dp), (i, j, k)))
 
 
@ipywidgets.interact(flame=ipywidgets.IntSlider(min=0, max=len(film) - 1))
def show_table_transition(flame: int) -> None:
    dp, (i, j, k) = film[flame]
    table = pd.DataFrame(dp)
    with pd.option_context("display.float_format", "{:.0g}".format):
        table = table.style.set_properties(
            subset=pd.IndexSlice[i + 1, j], **{"background-color": "#FF7000"}
        ).set_properties(
            subset=pd.IndexSlice[i, j - k * a[i]], **{"background-color": "#FFBF00"}
        )
        display(table)

計算量の改善

  • dp テーブルにもっと情報を与えたい
    • 作れる場合にどれだけ aia_{i} が余っているかを持たせる
dp[i][j]:=i番目まででjを作る際に余る最大のi番目の個数（作れない場合は−1）dp[i+1][j]={mi(dp[i][j]≥0)−1(j<aiまたはdp[i+1][j−ai]≦0)dp[i+1][j−ai]−1(それ以外)\begin{aligned} dp[i][j] &:= i番目まででjを作る際に余る最大のi番目の個数（作れない場合は-1）\\ dp[i+1][j] &= \begin{cases} m_{i} (dp[i][j] \ge 0)\\ -1 (j<a_{i}またはdp[i+1][j-a_{i}]\leqq 0)\\ dp[i+1][j-a_{i}]-1 (それ以外)\\ \end{cases} \end{aligned} 
# 個数制限付き部分和問題
 
n: int = 3
K: int = 17
a: list[int] = [3, 5, 8]
m: list[int] = [3, 2, 2]
 
dp: list[list[int]] = [[-1 for _ in range(K + 1)] for _ in range(n + 1)]
dp[0][0] = 0
 
film = [(copy.deepcopy(dp), (0, 0, 0))]
for i in range(n):
    for j in range(K + 1):
        if dp[i][j] >= 0:
            dp[i + 1][j] = m[i]
        elif j < a[i] or dp[i + 1][j - a[i]] <= 0:
            dp[i + 1][j] = -1
        else:
            dp[i + 1][j] = dp[i + 1][j - a[i]] - 1
 
        film.append((copy.deepcopy(dp), (i, j, k)))
 
 
@ipywidgets.interact(flame=ipywidgets.IntSlider(min=0, max=len(film) - 1))
def show_table_transition(flame: int) -> None:
    dp, (i, j, k) = film[flame]
    table = pd.DataFrame(dp)
    with pd.option_context("display.float_format", "{:.0g}".format):
        table = table.style.set_properties(
            subset=pd.IndexSlice[i + 1, j], **{"background-color": "#FF7000"}
        )
        if dp[i][j] >= 0:
            table.set_properties(
                subset=pd.IndexSlice[i, j], **{"background-color": "#FFBF00"}
            )
        if not (j < a[i] or dp[i + 1][j - a[i]] <= 0):
            table.set_properties(
                subset=pd.IndexSlice[i + 1, j - a[i]], **{"background-color": "#FFBF00"}
            )
        display(table)

最長部分増加列問題

dp[i]:=最後がaiであるような最長の増加部分列の長さdp[i]=max⁡{1,dp[j]+1∣j<iかつaj<ai}\begin{aligned} dp[i] &:= 最後がa_{i}であるような最長の増加部分列の長さ\\ dp[i] &= \max\{1, dp[j]+1|j<iかつa_{j}<a_{i}\}\\ \end{aligned} 
# 最長部分増加列問題
n: int = 5
a: list[int] = [4, 2, 3, 1, 5]
 
dp: list[int] = [0] * n
 
film = [(copy.deepcopy(dp), (0, 0))]
for i in range(n):
    dp[i] = 1
    for j in range(i):
        if a[j] < a[i]:
            dp[i] = max(dp[i], dp[j] + 1)
        film.append((copy.deepcopy(dp), (i, j)))
 
 
@ipywidgets.interact(flame=ipywidgets.IntSlider(min=0, max=len(film) - 1))
def show_table_transition(flame: int) -> None:
    dp, (i, j) = film[flame]
    table = pd.DataFrame([dp])
    with pd.option_context("display.float_format", "{:.0g}".format):
        table = table.style.set_properties(
            subset=pd.IndexSlice[0, i], **{"background-color": "#FF7000"}
        ).set_properties(subset=pd.IndexSlice[0, j], **{"background-color": "#FFBF00"})
        display(table)

計算問題に対する DP

分割数

dp[i][j]:=jのi分割の総数dp[i][0]=0dp[0][0]=1dp[i][j]=dp[i−1][j]+dp[i][j−i]\begin{aligned} dp[i][j] &:= jのi分割の総数 \\ dp[i][0] &= 0 \\ dp[0][0] &= 1 \\ dp[i][j] &= dp[i-1][j]+dp[i][j-i] \end{aligned}

dp[i][j]dp[i][j] を整数 jj を ii 個以下に分割するパターン数とすると、dp[i][j]dp[i][j]は、

  • jj を i−1i-1 個以下に分割するパターン
  • jj を ii 個に分割するパターン

に分類することができる。

前者については、dp[i−1][j]dp[i-1][j] の定義そのものである。
後者については、まず ii 個の箱に 1 つずつ割り当てておいて、残った j−ij-i 個を ii 個以下に分割するパターンを考えればよいので dp[i][j−i]dp[i][j-i] と表現できる。

以上より、dp[i][j]=dp[i−1][j]+dp[i][j−i]dp[i][j] = dp[i-1][j] + dp[i][j-i]

# 分割数
import functools
 
MOD: int = 998244353
 
 
@functools.cache
def dp(i, j):
    """
    dp[i][j] := 整数jをi個以下に分割する場合の数
    """
    if i == 0:
        return j == 0
    if j - i >= 0:
        return dp(i - 1, j) + dp(i, j - i) % MOD
    else:
        return dp(i - 1, j)

重複組み合わせ

dp[i][j]:=i番目までの品物からj個選ぶ組み合わせの総数dp[i][0]=0dp[i+1][j]=∑k=0min⁡(j,a[i])dp[i][j−k]\begin{aligned} dp[i][j] &:= i番目までの品物からj個選ぶ組み合わせの総数 \\ dp[i][0] &= 0 \\ dp[i+1][j] &= \sum_{k=0}^{\min(j,a[i])}dp[i][j-k] \\ \end{aligned} 
# 重複組み合わせ（ナイーブ解）
n: int = 3
m: int = 3
a: list[int] = [1, 2, 3]
 
dp = [[0 for _ in range(m + 1)] for _ in range(n + 1)]
dp[0][0] = 1
 
film = [(copy.deepcopy(dp), (0, 0, 0))]
for i in range(n):
    for j in range(m + 1):
        for k in range(min(j, a[i]) + 1):
            dp[i + 1][j] += dp[i][j - k]
            film.append((copy.deepcopy(dp), (i, j, k)))
 
 
@ipywidgets.interact(flame=ipywidgets.IntSlider(min=0, max=len(film) - 1))
def show_table_transition(flame: int) -> None:
    dp, (i, j, k) = film[flame]
    table = pd.DataFrame(dp)
    with pd.option_context("display.float_format", "{:.0g}".format):
        table = table.style.set_properties(
            subset=pd.IndexSlice[i + 1, j], **{"background-color": "#FF7000"}
        ).set_properties(
            subset=pd.IndexSlice[i, j - k], **{"background-color": "#FFBF00"}
        )
        display(table)
 
# 重複組み合わせ（ナイーブ解・組み合わせの要素）
n: int = 3
m: int = 3
a: list[int] = [1, 2, 3]
 
dp = [[[] for _ in range(m + 1)] for _ in range(n + 1)]
dp[0][0].append("")
 
film = [(copy.deepcopy(dp), (0, 0, 0))]
for i in range(n):
    for j in range(m + 1):
        for k in range(min(j, a[i]) + 1):
            for e in dp[i][j - k]:
                dp[i + 1][j].append(e + str(i) * k)
                film.append((copy.deepcopy(dp), (i, j, k)))
 
 
@ipywidgets.interact(flame=ipywidgets.IntSlider(min=0, max=len(film) - 1))
def show_table_transition(flame: int) -> None:
    dp, (i, j, k) = film[flame]
    table = pd.DataFrame(dp)
    with pd.option_context("display.float_format", "{:.0g}".format):
        table = table.style.set_properties(
            subset=pd.IndexSlice[i + 1, j], **{"background-color": "#FF7000"}
        ).set_properties(
            subset=pd.IndexSlice[i, j - k], **{"background-color": "#FFBF00"}
        )
        display(table)
dp[i][j]:=i番目までの品物からj個選ぶ組み合わせの総数dp[i][0]=1dp[i+1][j]=∑k=0min⁡(j,a[i])dp[i][j−k]=∑k=0min⁡(j−1,a[i])dp[i][j−1−k]+dp[i][j]−dp[i][j−1−ai]=dp[i+1][j−1]+dp[i][j]−dp[i][j−1−ai]\begin{aligned} dp[i][j] &:= i番目までの品物からj個選ぶ組み合わせの総数 \\ dp[i][0] &= 1 \\ dp[i+1][j] &= \sum_{k=0}^{\min(j,a[i])}dp[i][j-k] \\ &= \sum_{k=0}^{\min(j-1,a[i])}dp[i][j-1-k]+dp[i][j]-dp[i][j-1-a_{i}] \\ &= dp[i+1][j-1]+dp[i][j]-dp[i][j-1-a_{i}] \end{aligned}

参考: 蟻本 p.67 / 個人的な競プロメモ (opens in a new tab)

# 重複組み合わせ
n: int = 4
m: int = 4
a: list[int] = [1, 2, 3, 2]
 
MOD: int = 998244353
 
dp = [[0 for _ in range(m + 1)] for _ in range(n + 1)]
for i in range(n + 1):
    dp[i][0] = 1
 
film = [(copy.deepcopy(dp), (0, 1))]
for i in range(n):
    for j in range(1, m + 1):
        if j - 1 - a[i] >= 0:
            dp[i + 1][j] = (dp[i + 1][j - 1] + dp[i][j] - dp[i][j - 1 - a[i]]) % MOD
        else:
            dp[i + 1][j] = (dp[i + 1][j - 1] + dp[i][j]) % MOD
        film.append((copy.deepcopy(dp), (i, j)))
 
 
@ipywidgets.interact(flame=ipywidgets.IntSlider(min=0, max=len(film) - 1))
def show_table_transition(flame: int) -> None:
    dp, (i, j) = film[flame]
    table = pd.DataFrame(dp)
    with pd.option_context("display.float_format", "{:.0g}".format):
        table = (
            table.style.set_properties(
                subset=pd.IndexSlice[i + 1, j], **{"background-color": "yellow"}
            )
            .set_properties(
                subset=pd.IndexSlice[i + 1, j - 1], **{"background-color": "red"}
            )
            .set_properties(subset=pd.IndexSlice[i, j], **{"background-color": "red"})
        )
        if j - 1 - a[i] >= 0:
            table.set_properties(
                subset=pd.IndexSlice[i, j - 1 - a[i]], **{"background-color": "blue"}
            )
        display(table)